Як знайти площу трикутника

Знайомство з геометрією починається в 7 класі. Закладені на цьому етапі знання, стануть в нагоді і в дорослому житті, якщо людина надалі захоче зайнятися вивченням точних наук. Вивчаючи властивості фігур, доведеться зіткнутися з трикутником і навчитися обчислювати його площу.

Перед тим як знайти площу трикутника, необхідно ближче познайомитися з його особливостями.

Підписуйтесь на наш Telegram – канал

Зміст:

1. Що таке «трикутник»
2. Як розрахувати площу трикутника
3. Як розрахувати площу рівнобедреного трикутника
4. Як знайти площу рівностороннього трикутника
5. Як обчислити площу прямокутного трикутника
6. Як знайти площу трикутника за трьома сторонами
7. Як знайти площу трикутника через кути
8. Як прищепити школяреві любов до геометрії

Що таке «трикутник»

Трикутник – це геометрична фігура, що складається з трьох точок, що лежать на одній прямій, і трьох відрізків, які попарно з’єднують ці точки. Відрізки називаються – сторонами, а точки – вершиною. Трикутники відрізняються за величиною кута:

1. Гострокутні.
2. Прямокутні.
3. Тупокутні.

Розрізняються трикутники і по довжині сторін:

1. Рівносторонні – три рівні сторони.
2. Рівнобедрені – дві рівні сторони.
3. Різнобічні – три сторони з різною довжиною.

Площа кожної фігури розраховується різними способами: за двома, трьома сторонами, по формулі Герона, через основу і висоту. Розібравшись один раз, надалі це не буде викликати труднощів, адже геометрія буде супроводжувати школяра до випускного, а потім також продовжиться в університеті.

Сьогодні існують онлайн-калькулятори, що дозволяють проводити розрахунки, але перш ніж скористатися таким помічником, необхідно розібратися в позначеннях і формулах. Без базових знань не вийде зробити правильні розрахунки.

Як розрахувати площу трикутника

Один з найвідоміших і популярних методів розрахунку – це по основі і висоті. Для цього необхідно основу і висоту помножити один на одного, а потім розділити навпіл.

Формула: S = a*h

Де «а» – це основа трикутника, «h» – висота трикутника. Скористаємося формулою на прикладі. Нам дана фігура з основою 6 см і заввишки 4 см.

Насамперед множимо два відомих значення між собою та отримуємо площу шуканої фігури: S = 6*4 = 12 см.

Як розрахувати площу рівнобедреного трикутника

Щоб обчислити площу рівнобедреного трикутника доведеться скористатися класичною формулою, яка була представлена ​​вище: S = ah. Щоб визначити висоту знадобиться звернутися до теореми Піфагора або розрахувати за формулою Герона, про яку ми розповімо далі.

Формула для обчислення площі виглядає наступним чином.

Застосовуючи формулу для обчислення площі через сторони та основу, знадобиться звернутися до теореми Піфагора.

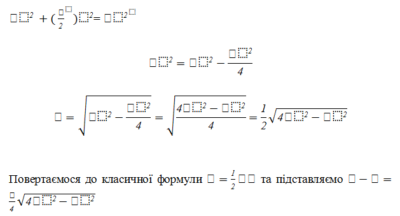
Повертаємося до класичної формули  та підставляємо

Як знайти площу рівностороннього трикутника

Таку фігуру також називають правильною. Для розрахунків необхідно скористатися класичною формулою та підставити обчислення висоти рівностороннього трикутника.

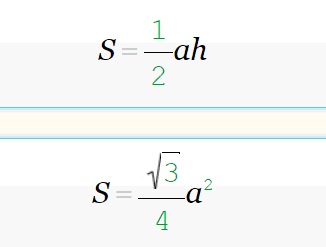
Наприклад, дотримуючись представленої формули, обчислимо сторону (а) рівну 5. У результаті отримаємо такі значення:

1. Сторона a = 5
2. Площа S = 10.8253

Як обчислити площу прямокутного трикутника

У прямокутному трикутнику одна з вершин завжди залишається рівною 90°. Щоб провести розрахунки знадобиться класична формула.

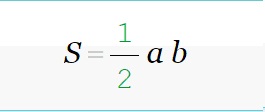
Приклад:

Необхідно обчислити площу прямокутного трикутника з двома катетами: a = 9 см, b = 5 см. Виконуємо розрахунок: S = (9*5) / 2 = 22,5 см.

Також для вирішення можна застосувати теорему Піфагора вона діє в тому випадку, якщо нам відомий тільки один катет.

Як знайти площу трикутника за трьома сторонами

Представлено безліч варіантів для розрахунку довжини сторін радіусу та площі трикутника. Одна зі зручних формул для розрахунку площі по трьох сторонах називається формулою Герона та використовується в тому випадку, якщо відома довжина всіх трьох сторін. Як виглядає формула:

Півпериметром називають суму довжин усіх сторін розділену на 2.

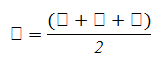
Розглянемо формулу на прикладі. Нам необхідно знайти півпериметр трикутника, де дані такі сторони a = 5, b = 6, c = 7. Виконуємо розрахунок:

1. P = (5 + 6 + 7) / 2 = 9
2. 
3. Площа трикутника дорівнює 14,7 см.

Обчислюючи за формулою Герона, спочатку ми перемножили отримані результати, потім з отриманого числа витягли квадратний корінь. Кінцеве значення і є площею шуканого трикутника.

Для повного розуміння необхідно постійно тренуватися та займатися. З кожним разом ускладнюйте завдання та вибирайте приклади з іншими значеннями. Систематичне повторення дозволить напам’ять вивчити формулу Герона та навчитися застосовувати її для вирішення простих і складних завдань.

Геометрія може стати в нагоді не тільки в школі, але і в дорослому житті, наприклад, тим, хто займається облаштуванням інтер’єру, ремонтами та планує вивчати архітектуру.

Як знайти площу трикутника через кути

Для оперування цією формулою необхідно знати суму двох сторін і кут, який проходить між ними. Знаючи ці дані, вдасться обчислити площу трикутника.

Формула:

S = a * b * sin (y)

S = a * b * sin (β)

S = a * b * sin (α)

Де a, b – сторони трикутника

α – кут між сторонами.

Розглянемо на прикладі

Дані сторони a = 4, b = 5, і кут γ = 60°. Щоб дізнатися синус кута 60° необхідно звернутися до таблиці синусів. Синус 60° = 0,8

S = 4 * 5 * 60° = 8 кв.см

Зустрічаються й інші ситуації, коли в умові позначена сторона та потрібно дізнатися кут. Для цього використовують класичні формули, оскільки сума всіх кутів трикутника становить 180 градусів.

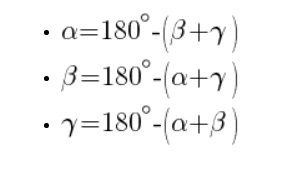
У міру отримання знань, рівень завдань буде ускладнюватися, а з приходом тригонометрії доведеться вправлятися ще більше, щоб розуміти, як робити обчислення. Тому, щоб і далі не зазнавати труднощів з геометрією, необхідно не запускати предмет і знати основи, по ходу навчання все буде базуватися саме на них.

Як прищепити школяреві любов до геометрії

Не розібравшись в одній темі, не можна перескакувати на іншу. Через деякий час виявиться, що брак знань заважає подальшому розумінню точних наук. Бажано повернутися саме до того моменту, коли матеріал виявився незрозумілим і приділити йому достатньо уваги: ​​вивчити теореми та потренуватися на прикладах.

Крім запам’ятовування аксіом, теорем та формул, необхідно розуміти, як фігури утворюються на площині. З ускладненням програми знадобляться знання про двомірні фігури. Знаючи про це, стане зрозуміло, що будь-яку складну фігуру можна розділити на прості фігури. Це допоможе у вирішенні навіть найскладніших завдань.

В першу чергу, зробіть упор на вивчення, розпізнавання фігур та їх геометричні властивості. Без простих знань, буде складно просуватися далі. У разі необхідності зверніться до репетитора або знайдіть в інтернеті онлайн-курс.

Через деякий час ви без проблем будете знати, як розрахувати площу трикутника.