Как найти площадь треугольника

Знакомство с геометрией начинается в 7 классе. Заложенные на этом этапе знания, пригодятся и во взрослой жизни, если человек в дальнейшем захочет заняться изучением точных наук. Изучая свойства фигур, придется столкнуться с треугольником и научиться вычислять его площадь.

Перед тем как найти площадь треугольника, необходимо ближе познакомиться с его особенностями.

Подписывайтесь на наш Telegram — канал

Содержание:

1. Что такое «треугольник»
2. Как рассчитать площадь треугольника
3. Как рассчитать площадь равнобедренного треугольника
4. Как найти площадь равностороннего треугольника
5. Как вычислить площадь прямоугольного треугольника
6. Как найти площадь треугольника по трем сторонам
7. Как найти площадь треугольника через углы
8. Как привить школьнику любовь к геометрии

Что такое «треугольник»

Треугольник – это геометрическая фигура, состоящая из трех точек, лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки. Отрезки именуются – сторонами, а  точки – вершиной. Треугольники отличаются по величине угла:

1. Остроугольные.
2. Прямоугольные.
3. Тупоугольные.

Различаются треугольники и по длине сторон:

1. Равносторонние – три равных стороны.
2. Равнобедренные – две равных стороны.
3. Разносторонние ‒ три стороны с разной длиной.

Площадь каждой фигуры рассчитывается разными способами: по двум, трем сторонам, по формуле Герона, через основание и высоту. Разобравшись один раз, в дальнейшем это не будет вызывать трудностей, ведь геометрия будет сопровождать школьника до выпускного, а потом продолжится в университете.

Сегодня существуют онлайн-калькуляторы, позволяющие производить расчеты, но прежде чем воспользоваться таким помощником, необходимо разобраться в обозначениях и формулах. Без базовых знаний не получится произвести правильные расчеты.

Как рассчитать площадь треугольника

Один из самых известных и популярных методов расчёта ‒ это по основанию и высоте.  Для этого необходимо основание и высоту умножить друг на друга, а потом разделить пополам.

Формула: S = a*h

Где «а» – это основание треугольника, «h» ‒ высота треугольника. Воспользуемся формулой на примере. Нам дана фигура с основанием 6 см и высотой 4 см.

Первым делом умножаем два известных значения между собой и получаем площадь искомой фигуры: S =  6*4 = 12 см.

Как рассчитать площадь равнобедренного треугольника

Чтобы вычислить площадь равнобедренного треугольника придется воспользоваться классической формулой, которая была представлена выше: S =  ah. Чтобы определить высоту понадобится обратиться к теореме Пифагора или рассчитать по формуле Герона, о которой мы расскажем дальше.

Формула для вычисления площади выглядит следующим образом.

Применяя формулу для вычисления площади через стороны и основание, понадобится обратиться к теореме Пифагора.

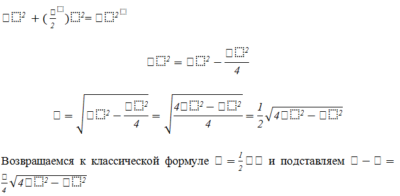
Возвращаемся к классической формуле  и подставляем

Как найти площадь равностороннего треугольника

Такую фигуру также называют правильной. Для расчетов необходимо воспользоваться классической формулой и подставить вычисление высоты равностороннего треугольника.

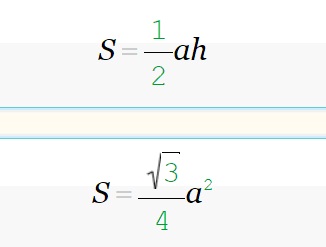
Например, придерживаясь представленной формулы, вычислим сторону (а) равную 5. В результате получим следующие значения:

1. Сторона a = 5
2. Площадь S = 10.8253

Как вычислить площадь прямоугольного треугольника

В прямоугольном треугольнике одна из вершин всегда остается равной 90°. Чтобы произвести расчёты понадобится классическая формула.

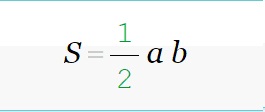
Пример:

Необходимо вычислить площадь прямоугольного треугольника с двумя катетами: a = 9 см, b = 5 см. Производим расчет: S =  (9*5) / 2 = 22,5 см.

Также для решения можно применить теорему Пифагора она действует в том случае, если нам известен только один катет.

Как найти площадь треугольника по трем сторонам

Представлено множество вариантов для расчёта длины сторон радиуса и площади треугольника. Одна из удобных формул для расчёта площади по трём сторонам называется формулой Герона и используется в том случае, если известна длина всех трех сторон.

Полупериметром называют сумму длин всех сторон разделенную на 2.

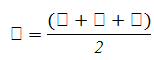
Рассмотрим формулу на примере. Нам необходимо найти полупериметр треугольника, где даны следующие стороны  a = 5, b = 6, c = 7. Производим расчет:

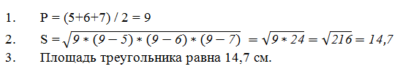
Вычисляя по формуле Герона, вначале мы перемножили полученные результаты, затем из полученного числа извлекли квадратный корень. Конечное значение и является площадью искомого треугольника.

Для полного понимания необходимо постоянно упражняться и заниматься. С каждым разом усложняйте задачу и выбирайте примеры  с другими значениями.  Систематическое повторение позволит назубок выучить формулу Герона и научиться применять её для решения простых и сложных задач.

Геометрия может пригодиться не только в школе, но и во взрослой жизни, например, тем, кто занимается обустройством интерьера, ремонтами и планирует изучать архитектуру.

Как найти площадь треугольника через углы

Для оперирования этой формулой необходимо знать сумму двух сторон и угол, который проходит между ними. Зная эти данные, удастся вычислить площадь треугольника.

Формула:

S =  a * b * sin (y)

S =  a * b * sin (ϐ)

S =  a * b * sin (α)

Где a, b – стороны треугольника

α – угол между сторонами.

Рассмотрим на примере

Даны стороны a = 4, b = 5, и угол γ = 60°. Чтобы узнать синус угла 60° необходимо обратиться к таблице синусов. Синус 60° = 0,8

S =  4 * 5 * 60° = 8 кв.см

Встречаются и другие ситуации, когда в условии обозначена сторона и нужно узнать угол. Для этого используют классические формулы, так как сумма всех углов треугольника составляет 180 градусов.

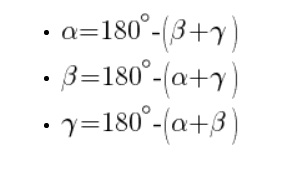
По мере получения знаний, уровень задач будет усложняться, а с приходом тригонометрии придется упражняться ещё больше, чтобы понимать, как производить вычисления. Поэтому, чтобы и дальше не испытывать сложности с геометрией, необходимо не запускать предмет и знать основы, по ходу учебы всё будет базироваться именно на них.

Как привить школьнику любовь к геометрии

Не разобравшись в одной теме, нельзя перескакивать на другую. Через некоторое время обнаружится, что недостаток знаний мешает дальнейшему постижению точных наук.  Желательно вернуться именно к тому моменту, когда материал оказался непонятным и уделить ему достаточное внимание: выучить теоремы и потренироваться на примерах.

Кроме запоминания аксиом, теорем и формул, необходимо понимать, как фигуры образуются на плоскости. С усложнением программы понадобятся знания о двухмерных фигурах. Зная об этом, станет понятно, что любую сложную фигуру можно разделить на простые фигуры. Это поможет в решении даже самых сложных задач.

В первую очередь, делайте упор на изучение, распознавание фигур и их геометрические свойства. Без простых знаний, будет сложно продвигаться дальше. В случае необходимости обратитесь к репетитору или найдите в интернете онлайн-курс.

Через некоторое время вы без проблем будете знать, как рассчитать площадь треугольника.